问题
问答题
证明：xn+xn-1+…+x=1(n＞1)在(0，1)内必有唯一实根xn，并求
．
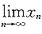答案
参考答案：设fn(x)=xn+xn-1+…+x-1，fn(0)=-1，fn(1)=n-1＞0，
而fn(x)连续，则由介值定理可得fn(x)在(0，1)内有零点．
又fn’(x)=nxn-1+(n-1)xn-2+…+1＞0，则fn(x)单调增加，
所以fn(x)在(0，1)内有唯一零点，记为xn．于是有
， ①
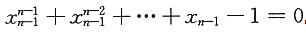． ②
式①-式②得
．
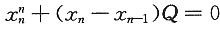由于Q内均是正项，故Q＞0，又
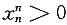，所以
xn-xn-1＜0，即xn＜xn-1，即{xn}单调递减且有下界，故有极限，设为a．
由式①可得
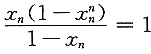，即
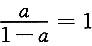，解之得
．
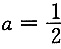