根据句意及首字母提示在横线处填上恰当的单词,使句子意思完整,语法正确。
1. There are three s_______in my study. There are many kinds of books on them.
2. The dictionary is h_______to us. I think you should buy it.
3. I don't want to take part in Mary's party, so I_______her invitation.
4. My old shoes h_______my foot, so I've to buy a new pair.
5. She c_______her face with her hands just now. She seemed to have cried.
6. My mother always t_______us like children.
7. I think you should put a f________book near your bed. If you have any problems, you can read it.
8. He is a good and famous writer. A new book came o _____last week again,
9. If you cut yourself by accident, you should p_______the cut hard.
10. If you fell d________by accident and wasn't able to move, you should call the hospital first.
 ,且f(x,0)=1,f’y(x,0)=x,则f(x,y)=______.
,且f(x,0)=1,f’y(x,0)=x,则f(x,y)=______.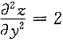 ,可得
,可得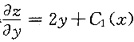 ,由
,由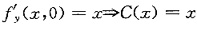 ,即
,即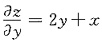 ,积分得z=y2+xy+C2(y),
,积分得z=y2+xy+C2(y),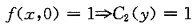 ,故z=y2+xy+1.
,故z=y2+xy+1. ,且f(x,0)=1,f’y(x,0)=x,则f(x,y)=______.
,且f(x,0)=1,f’y(x,0)=x,则f(x,y)=______.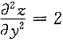 ,可得
,可得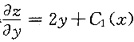 ,由
,由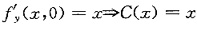 ,即
,即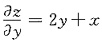 ,积分得z=y2+xy+C2(y),
,积分得z=y2+xy+C2(y),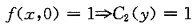 ,故z=y2+xy+1.
,故z=y2+xy+1.