问题
单项选择题
设函数f(x)，g(x)在a点的某邻域内二阶可导，且f(a)=g(a)=0，f’(a)＜0．g’(a)＞0，令
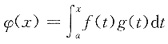，则
A．x=a是φ(x)的极小值点．
B．x=a是φ(x)的极大值点．
C．(a，φ(a))是曲线y=φ(x)的拐点．
D．以上都不对．
答案
参考答案：C
解析：[详解] φ’(x)=f(x)g(x)，则
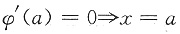是φ(x)的驻点，
又φ"(a)=[f(x)g’(x)+f’(x)g(x]|x=a=f(a)g’(a)+f’(a)g(a)=0．
φ"(a)=[f(x)g"(x)+f"(x)g(x)+2f’(x)g’(x)]|x=a
=-f(a)g"(a)+f"(a)g(a)+2f’(a)g’(a)=2f’(a)g’(a)＜0，
所以(a，φ(a))是曲线y=φ(x)的拐点，应选(C)．