若定义在（-∞，1）∪（1，+∞）上的函数y=f（x）满足f（x+2）=f（-x

问题选择题

若定义在（-∞，1）∪（1，+∞）上的函数y=f（x）满足f（x+2）=f（-x），且当x∈（1，+∞）时，f(x)=|

2x-3

x-1

|，则下列结论中正确的是（　　）

A．存在t∈R，使f（x）≥2在[t-

，t+

]恒成立

B．对任意t∈R，0≤f（x）≤2在[t-

，t+

]恒成立

C．对任意t∈R^-，f（x）在[t-

，t+

]上始终存在反函数

D．对任意t∈R⁺，f（x）在[t-

，t+

]上始终存在反函数

答案

解：∵函数y=f（x）满足f（x+2）=f（-x），

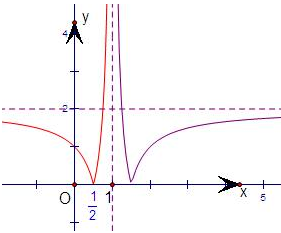
∴函数y=f（x）的图象关于x=1对称，且当x∈（1，+∞）时，f（x）=，作出函数f（x）的图象，如图所示．观察图象得：

A：不存在t∈R，使f（x）≥2在长度为1的区间上恒成立；故A错．

B：对任意t∈R，0≤f（x）≤2在[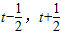 ]不是恒成立；故B错．

C：任意t∈R^-，f（x）在[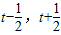 ]上始终是单调函数，故存在反函数；C正确．

D：对任意t∈R⁺，f（x）在[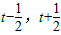]上不是始终是单调的，不一定存在反函数；故D错．

故选C．