【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…
【流程图】
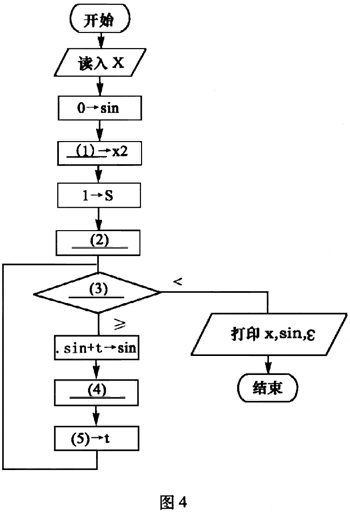
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
参考答案:x*x (2)x->t (3)│t│:ε (4)s+2->s
(5)(-1) * t* x2/(s* (s-1))
解析: 该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值,变量s和变量x2的作用是什么呢从流程图的功能上看,需要计算11、3!、5!,……,又从变量s的初值置为1可知,变量s主要用来计算这此数的阶乘的,但没有其他变量用于整数自增,这样就以判断s用来存储奇数的,即s值依次为1、3、5,……。但x2的功能还不明确,现在可以不用管它。
(2)空的作用是给t赋初值,即给它多项式的第一项,因此应填写“x->t”。(3)空处需填写循环条件,显然当t的绝对值小于ε(>0)就表示已经达到误差要求,因此(3)空应填入“│t│:ε”。由变量s的功能可知,(4)空应当实现变量s的增加,因此(4)空应填入“s+2->s”。 (5)空应当是求多项式下一项的值,根据多项式连续两项的关系可知,当前一项为t时,后一项的值为(-1)*t*x*x/(s*(s-1))。但这样的话,每次循环都需要计算一次x*x,计算效率受到影响,联想到变量x2还没用,这时就可以判断x2就是用来存储x*x的值,使得每次循环者少进行一次乘法运算。因此(1)空处应填入“x*x”,(5)空处应填入“(-1)*t*x2/(s*(s-1))”。
