问题
填空题
设直线
在平面x+y+z=0上的投影为直线L，则点(1，2，1)到直线L的距离等于______。
答案
参考答案：
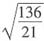
解析：[考点] 点到直线的距离
过直线
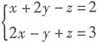的平面束为(x+2y-z-2)+k(2x-y+z-3)=0，即(1+2k)x+(2-k)y+(k-1)z-2-3k=0，由{1+2k，2-k，k-1}·{1，1，1}=0，
得k=-1，
则投影直线为L：
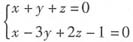，S={1，1，1}×{1，-3，2}={5，-1，-4}。
对称式方程为L：
。
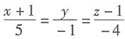令M0M1的坐标分别为(-1，0，1)，(1，2，1)，
={2，2，0}，则d=
。
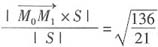