问题
问答题
设二次型
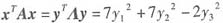其中-2是二次型矩阵A的一个特征值。
试用正交变换将二次型-厂化为标准形，并写出所用正交变换；
答案
参考答案：二次型f的矩阵
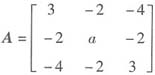
由λ=-2是A的特征值，
得到a=6。
由矩阵A的特征多项式
，
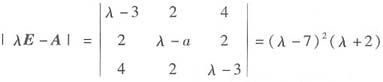得到矩阵A的特征值是λ1=λ2=7，λ3=-2。
对λ=7，解齐次方程组(7E-A)x=0得基础解系α1=(1，-2，0)T，α2=(1，0，-1)T，
对λ=-2，解齐次方程组(-2E-A)x=0得基础解系α3=(2，1，2)T。
因为α1，α2不正交，故需Schmidt正交化，有
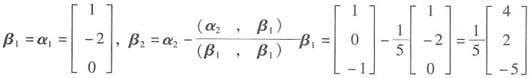
再单位化，得
那么令
，则在正交变换x=Qy下，有
。
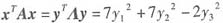