问题
问答题
设f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1.求证对任意的正数a和b,在(0,1)内存在ε≠η使得
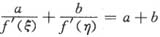 .
.
答案
参考答案:结论可改写为而[*].由于[*],又f(x)连续地从f(0)=0变到f(1)=1,从而存在c∈(0,1)使得[*],结论又可改写为[*],再把f(0)=0与f(1)=1用上,上式就可改写成
[*]
这提示我们在使[*]的c处分割区间[0,1],然后分别在[0,c]与[c,1]上应用拉格朗日中值定理.
因f(0)=0,f(1)=1,又[*],从而[*]是f(x)的值域[0,1]内的一点.由连续函数的性质知[*]c∈(0,1)使[*].分别在区间[0,c]与[c,1]上对f(x)应用拉格朗日中值定理即知:[*]使得
f(c)-f(0)=f’(ξ)(c-0)=cf’(ξ), (*)
又[*]使得
f(1)-f(c)=f’(η)(1-c)=(1-c)f’(η), (**)
把f(0)=0与f(1)=1以及[*]代入(*)与(**),分别得到
[*]
从而
[*]
