设常数a∈(-∞,+∞),讨论反常积分
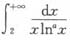 的敛散性.又当上述反常积分收敛时,记
的敛散性.又当上述反常积分收敛时,记
 ,确定当a取何值时I(a)取得最小值.
,确定当a取何值时I(a)取得最小值.
参考答案:当a≠1时
[*]
当a=1时
[*]
因此,当a≤1时广义积分发散,当a>1时广义积分收敛,且
[*]
记q=ln2,则常数q满足0>q>1.因为I(a)>0,故lnI(a)=-[ln(a-1)+(a-1)lnq],于是
[*]
这表明函数I(a)当[*]时取得最小值.
设常数a∈(-∞,+∞),讨论反常积分
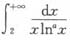 的敛散性.又当上述反常积分收敛时,记
的敛散性.又当上述反常积分收敛时,记
 ,确定当a取何值时I(a)取得最小值.
,确定当a取何值时I(a)取得最小值.
参考答案:当a≠1时
[*]
当a=1时
[*]
因此,当a≤1时广义积分发散,当a>1时广义积分收敛,且
[*]
记q=ln2,则常数q满足0>q>1.因为I(a)>0,故lnI(a)=-[ln(a-1)+(a-1)lnq],于是
[*]
这表明函数I(a)当[*]时取得最小值.