大宇公司2009年有一个投资机会,无风险的报酬率为4%,投资人要求的必要报酬率为10%,要求现金流变化系数在0.10—0.20区间,现金流标准差不高于600万元,有关资料如表所示(单位:万元):

要求:
(1)计算第1年和第2年现金流的标准差;
(2)计算项目现金流的标准差;
(3)计算项目现金流的变异系数;
(4)计算项目的期望净现值;
(5)判断该投资方案是否可行;
(6)如果第一年的肯定当量系数为0.8,第二年的肯定当量系数为0.85,用风险调整现金流量法判断项目是否可行;
(7)如果该公司考虑了悲观的情景,运用场景概况分析该方案是否可行。
参考答案:
(1)第1年现金流的期望值:3000×0.6+2000×0.4=2600(万元)
方差=(3000-2600)2×0.6+(2000-2600)2×0.4=96000+144000=240000
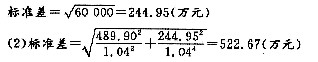
第2年现金流的期望值=2500×0.4+2000×0.6=2200(万元)
方差=(2500-2200)2×0.4+(2000-2200)2×0.6=36000+24000=60000
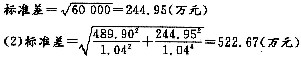
(3)第1年和第2年的现金流的期望值现值之和
=2600/1.04+2200/(1.04×1.04)
=4534.02(万元)
变异系数=522.67/4534.02=0.12
(4)期望净现值=4534.02-3000=1534.02(万元)
(5)由于该方案的期望净现值大于0,并且标准差和变化系数在可接受的范围之内,因此,该方案是可行的。
(6)风险调整后的净现值
=0.8×2600/(1+4%)+0.85×2200/(1+4%)2-3000=728.92(万元)>0,所以该方案可行。
(7)在悲观的情景下,各变量的预期值都是最悲观的估计,则
净现值=2000/(1+10%)+2000/(1+10%)2-3000=471.07(万元)>0,所以该方案可行。
