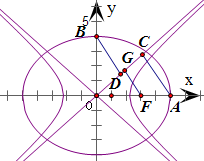
问题
选择题
离心率为
|
答案
设椭圆方程为
+x2 a2
=1(a>b>0),双曲线方程为y2 b2
-x2 m2
=1(m>0,n>0)y2 n2
它们一个公共的焦点为F(c,0)
∵椭圆长轴端点A到双曲线的渐近线nx-my=0的距离|AC|=
=an n2+m2
=2n,an c
椭圆短轴端点B到双曲线的渐近线nx-my=0的距离|BD|=bm c
椭圆焦点F到双曲线的渐近线nx-my=0的距离|FG|=
=n,cn c
∴2•
=2n+n,bm c
∵
=c a
,1 2
∴a=2c,
∴b=
=a2-c2
c,3
∴2
m=3n,3
∴m=
n,3 2
∴c=
=m2+n2
n,7 2
∴e=
=c m
=
n7 2
n3 2
.21 3
故选:C.