问题
问答题
设矩阵
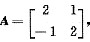 E为2阶单位矩阵,矩阵B满足BA=B+2E,B*是B的伴随矩阵,则|B|=______.
E为2阶单位矩阵,矩阵B满足BA=B+2E,B*是B的伴随矩阵,则|B|=______.
答案
参考答案:[解] 由矩阵方程BA=B+2E得B(A-E)=2E,两边取行列式有
|B(A-E)|=|2E|即|B||A-E|=22|E|=4
又因[*]故|B|=2.
利用|A*|=|A|n-1可知|B*|=|B|2-1=2.
解析:[评注] 本题不要去求矩阵B或B*,那样就走冤枉路了!
设矩阵
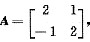 E为2阶单位矩阵,矩阵B满足BA=B+2E,B*是B的伴随矩阵,则|B|=______.
E为2阶单位矩阵,矩阵B满足BA=B+2E,B*是B的伴随矩阵,则|B|=______.
参考答案:[解] 由矩阵方程BA=B+2E得B(A-E)=2E,两边取行列式有
|B(A-E)|=|2E|即|B||A-E|=22|E|=4
又因[*]故|B|=2.
利用|A*|=|A|n-1可知|B*|=|B|2-1=2.
解析:[评注] 本题不要去求矩阵B或B*,那样就走冤枉路了!