问题
填空题
已知函数f(x)=x2-cosx,对于
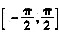 上的任意x1,x2,有如下条件:
上的任意x1,x2,有如下条件:
①x1>x2;
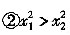 ;③|x1|>x2。
;③|x1|>x2。
其中能使f(x1)>f(x2)恒成立的条件序号是()。
答案
参考答案:②
解析:
函数f(x)=x2-cosx为偶函数,则[*],在区间[*]上,函数f(x)=x2-cosx为递增函数。所以[*][*]
已知函数f(x)=x2-cosx,对于
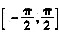 上的任意x1,x2,有如下条件:
上的任意x1,x2,有如下条件:
①x1>x2;
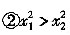 ;③|x1|>x2。
;③|x1|>x2。
其中能使f(x1)>f(x2)恒成立的条件序号是()。
参考答案:②
解析:
函数f(x)=x2-cosx为偶函数,则[*],在区间[*]上,函数f(x)=x2-cosx为递增函数。所以[*][*]