问题
解答题
(本小题满分8分)某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
⑴请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
⑵求自变量x的取值范围;
⑶怎样安排生产每天获得的利润最大,最大利润是多少?
答案
⑴此车间每天所获利润y(元)与x(人)之间的函数关系式是
y=6x·150+5(20-x)·260=26000-400x................. (3分)
⑵由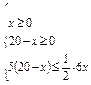 得;
得;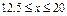
因为x为整数,所以x=13,14,…,20..................... (3分)
⑶∵y随x的增大而减小,
∴当x=13时,y最大=26000-400×13=20800
即安排13人生产甲种零件,安排7人生产乙种零件,所获利润最大,最大利润为20800元。
(
略
