问题
问答题
证明方程lnx=
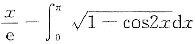在区间(0，+∞)内有且仅有两个不同实根．
答案
参考答案：记
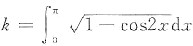＞0，方程化为lnx=
-k．
令f(x)=lnx-
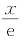+k，则f’(x)=
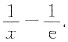由f’(x)=0解得唯一驻点x=e，且f’(x)在此由正变负，x=e是极大点也是最大点，最大值为f(e)=k＞0；又由
=-∞，
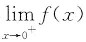=-∞，知f(x)在(0，e)与(e，+∞)各有且仅有一个零点，即f(x)在(0，+∞)有且仅有两个零点．
解析：[考点提示] 函数最大值的证明．