问题
问答题
在过点O(0,0)和A(π,0)的曲线y=asinx(a>0)中,求一条曲线L,使沿该曲线从O到A的积分
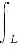 (1+y3)dx+(2x+y)dy的值最小.
(1+y3)dx+(2x+y)dy的值最小.
答案
参考答案:(1) 记曲线y=asinx(x∈[0,π])为La,则
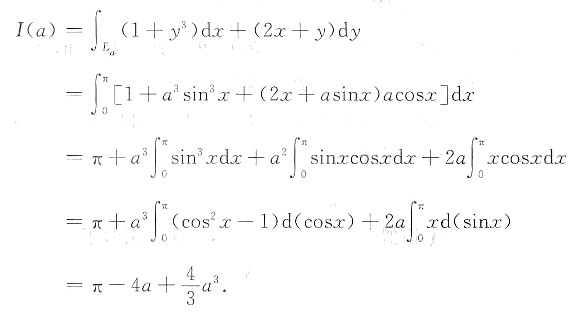
(2) 求I(a)的最小值点.
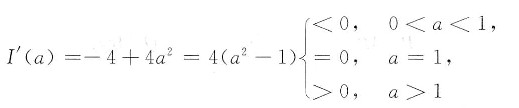
 I(a)在(0,+∞)上的最小值点是a=1.
I(a)在(0,+∞)上的最小值点是a=1.
因此所求曲线为y=sinx(0≤x≤π).
解析:[考点提示] 求曲线积分.
在过点O(0,0)和A(π,0)的曲线y=asinx(a>0)中,求一条曲线L,使沿该曲线从O到A的积分
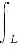 (1+y3)dx+(2x+y)dy的值最小.
(1+y3)dx+(2x+y)dy的值最小.
参考答案:(1) 记曲线y=asinx(x∈[0,π])为La,则
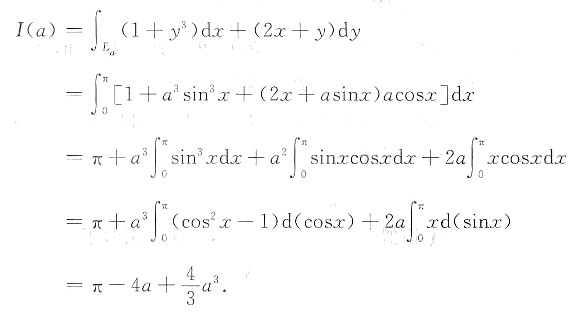
(2) 求I(a)的最小值点.
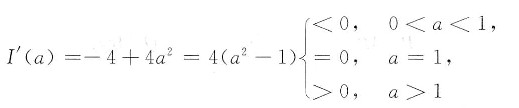
 I(a)在(0,+∞)上的最小值点是a=1.
I(a)在(0,+∞)上的最小值点是a=1.
因此所求曲线为y=sinx(0≤x≤π).
解析:[考点提示] 求曲线积分.