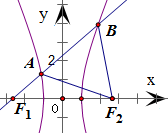
双曲线C：x2a2-y2b2=1的左右焦点分别为F1、F2，过F1的直线与双曲线

问题填空题

双曲线C：

=1的左右焦点分别为F₁、F₂，过F₁的直线与双曲线左右两支分别交于A、B两点，若△ABF₂是等边三角形，则双曲线C的离心率为______．

答案

根据双曲线的定义，可得|BF₁|-|BF₂|=2a，

∵△ABF₂是等边三角形，即|BF₂|=|AB|

∴|BF₁|-|BF₂|=2a，即|BF₁|-|AB|=|AF₁|=2a

又∵|AF₂|-|AF₁|=2a，

∴|AF₂|=|AF₁|+2a=4a，

∵△AF₁F₂中，|AF₁|=2a，|AF₂|=4a，∠F₁AF₂=120°

∴|F₁F₂|²=|AF₁|²+|AF₂|²-2|AF₁|•|AF₂|cos120°

即4c²=4a²+16a²-2×2a×4a×（-

）=28a²，解之得c=

a，

由此可得双曲线C的离心率e=

故答案为：