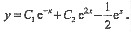问题
问答题
求微分方程y’’-y’-2y=ex的通解．
答案
参考答案：
对应的齐次方程为y’’-y’-2y=0，
特征方程r2-r-2=0，
特征根r1=-1，r2=2，
齐次方程通解为Y=C1e-x+C2e2x.
设原方程特解为y*=Aex代入原方程可得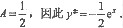
方程通解为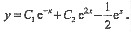
搜题请搜索小程序“爱下问搜题”
求微分方程y’’-y’-2y=ex的通解．
参考答案：
对应的齐次方程为y’’-y’-2y=0，
特征方程r2-r-2=0，
特征根r1=-1，r2=2，
齐次方程通解为Y=C1e-x+C2e2x.
设原方程特解为y*=Aex代入原方程可得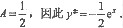
方程通解为