问题
填空题
设φ(u,v,w)有一阶连续偏导数且φ’2-φ’3≠0,z=z(x,y)是由φ(x2-y2,y2-z2,z2-x2)=0确定的函数,则当z≠0时
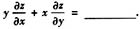
答案
参考答案:[*]
解析:[分析一] 方程两边求全微分得
φ’1·d(x2-y2)+φ’2·d(y2-z2)+φ’3·d(z2-x2)=0,
即φ’1·(2xdx-2ydy)+φ’2(2ydy-2zdz)+φ’3·(2zdz-2xdx)=0,
整理得x(φ’1-φ’3)dx+y(φ’2-φ’1)dy=z(φ’2-φ’3)dz,
于是[*]
由dx,dy的系数分别为[*]知
[*]
[分析二] 代公式,先分别求出[*]把方程记为F(x,y)=0,其中
F(x,y)=φ(x2-y2,y2-z2,z2-x2),
[*]
