问题
问答题
求幂级数
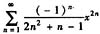的收敛半径R，收敛域D与和函数S(x)。
答案
参考答案：因在幂级数中所有奇次幂项系数为零，可直接求级数中后项与前项绝对值之比的极限，并利用比值判别法得出收敛半径，设x≠0，则
[*]
从而，当|x|＜1时幂级数绝对收敛，当|x|＞1时幂级数发散，其收敛半径R=1，当x=±1时幂级数成为交错级数[*]单调减少，且[*]，按莱布尼兹判别法知级数条件收敛，故幂级数[*]的收敛域D=[-1，1]。
设[*]注意
[*]
于是，分解原幂级数，可得
[*]
因[*]
故[*]
又因S2(0)=0，而当x≠O时
[*]
从而[*]
注意原幂级数当x=±1时收敛，而上面得到的和函数表达式在x=±1处也连续，因而和函数公式在点x=±1处也成立，即
[*]