问题
问答题
设函数f(x)在区间[0,1]上连续,且
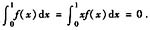 求证:存在满足0<ξ<η<1的ξ与η,使得f(ξ)=f(η)=0。
求证:存在满足0<ξ<η<1的ξ与η,使得f(ξ)=f(η)=0。
答案
参考答案:[证明一] 用反证法
若f(x)在(0,1)内没有零点,由f(x)在[0,1]上连续可知f(x)在(0,1)内或者恒正即f(x)>0,或者恒负即f(x)<0,显然这与[*]矛盾。
若f(x)在(0,1)内只有一个零点x0,这时只有两种情况:
[*]
在前一种情形下,当0<x<x0时同时有x-x0<0与f(x)<0,而当x0<x<1时同时有x-x0>0与f(z)>0,从而
[*]
这与[*]矛盾,在后一种情形下也可类似得出矛盾。
由此可见f(x)在(0,1)内至少有两个不同的零点,即存在满足0<ξ<η<1的ξ与η,使得f(ξ)=f(η)=0成立。
[证明二] 若在[0,1]上f(x)[*]0,则命题结论成立,设f(x)不恒为零,且
[*]
则F(0)=F(1)=0,又由F(x)在[0,1]上可导即知F’(x)=f(x),因此
[*]
由于F(x)为[0,1]上的连续函数,且[*]可知必定存在一点c∈(0,1),使F(c)=0,否则[*],与(*)式矛盾。
在[0,c],[c,1]上分别对F(x)应用罗尔定理,可知必定存在ξ∈(0,c),η∈(c,1),使得
F’(ξ)=f(ξ)=0,F’(η)=f(η)=0
