问题
问答题
设3阶矩阵A的三个特征值分别为-1，0，1，对应的特征向量分别为
α1=(a，a+3，a+2)T，α2=(a-2，-1，a+1)T，α3=(1，2a，-1)T，且有
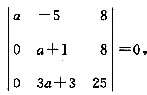试确定参数a的值，并求矩阵A．
答案
参考答案：[*]
当a=-1时，α1=(-1，2，1)T，α2=(-3，-1，0)T，α3=(1，-2，-1)T满足α1+α3=0，所以α1、α2、α3线性相关，这与α1、α2、α3是对应不同特征值的特征向量矛盾(因为不同特征值对应的特征向量线性无关)，因此a≠一1，故a=0．此时
α1=(0，3，2)T，α2=(-2，-1，1)T，α3=(1，0，-1)T．
[*]