问题
问答题
求函数y=2x3-3x2的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线．
答案
参考答案：
令y’=6x2-6x=0，得x=0或x=1，y"=12x-6=0，得x=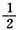
．
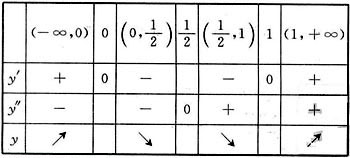
所以函数y的单调增区间为(-∞，0)和(1，+∞)，单调减区间为(0，1)；
函数y的凸区间为
，凹区间为
．
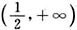故x=0时，函数有极大值0，x=1时，函数有极
小值-1，且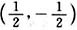点
为拐点，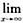
(2x3-3x2)不存在，且y=2x3-3x2没有无意义的点，故函数没有渐近线．