问题
选择题
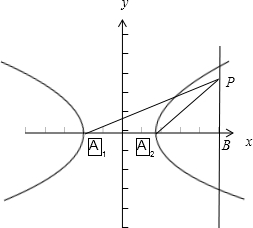
已知A1,A2分别是双曲线E:
|
答案
∵A1,A2分别是双曲线E:
-x2 a2
=1的左、右顶点,P为直线x=y2 b2
c(c为半焦距)上的一点,3 2
△A2PA1是底角为30°的等腰三角形,
∴|A1A2|=|PA2|=2a,
设直线x=
c交x轴于点B,则∠PA2B=60°,3 2
∴|A2B|=
|A2P|=a,1 2
∴2a=
c,即3c=4a,3 2
∴e=
=c a
.4 3
故选B.