问题
选择题
过双曲线
|
答案
由题意可得:双曲线的方程为
-x2 a2
=1,y2 b2
所以双曲线的渐近线方程为y=±
x.b a
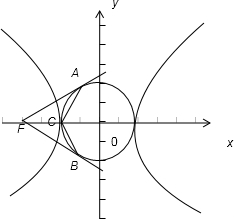
因为若∠ACB=120°,
所以根据图象的特征可得:∠AFO=30°,
所以c=2a,
又因为b2=c2-a2,
所以
=b a
,3
所以双曲线的渐近线方程为y=±
x.3
故选A.
过双曲线
|
由题意可得:双曲线的方程为
-x2 a2
=1,y2 b2
所以双曲线的渐近线方程为y=±
x.b a

因为若∠ACB=120°,
所以根据图象的特征可得:∠AFO=30°,
所以c=2a,
又因为b2=c2-a2,
所以
=b a
,3
所以双曲线的渐近线方程为y=±
x.3
故选A.