设函数f（x）=ax2+bx+c（a，b，c∈R），若x=-1为函数f（x）ex的一

问题单项选择题

设函数f（x）=ax²+bx+c（a，b，c∈R），若x=-1为函数f（x）e^x的一个极值点，则下列图象不可能为y=f（x）的图象是（）.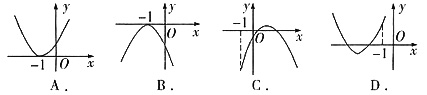

A.选项A

B.选项B

C.选项C

D.选项D

答案

参考答案：D

解析：

由y=f(x)e^x=e^x(ax²+bx+c)

y′=f′(x)e^x+e^xf(x)=e^x[ax²+(b+2a)x+b+c]，由x=-1为函数f(x)e^x的一个极值点可得，-1是方程ax²+(b+2a)x+b+c=0的一个根，所以有a-(b+2a)+b+c=0

c=a.

所以函数f(x)=ax²+bx+a，对称轴为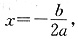且f(-1)=2a-b，f(0)=a．

对于A，由图得a＞0，f(0)＞0，f(-1)=0符合要求，对于B，由图得a＜0，f(0)＜0，f(-1)=0不矛盾，对于C，由图得a＜0，f(0)＜0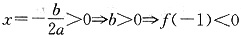，不矛盾，对于D，由图得a＞0，f(0)＞0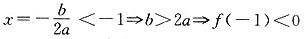，于原图中f(-1)＞0矛盾，D不对，故选D．