参考答案：由通解可知，特征根λ₁=1，λ₂=-1．于是特征方程为
(λ-1)(λ+1)=λ²-1=0，
故对应的齐次方程为y"-y=0．
该非齐次方程设为
y"-y=f(x)，其中f(x)为其非齐次项．由其通解知

为其一特解，将其代入y"-y，得到f(x)=(y^*)"-y^*，即

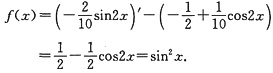
故所求方程为y"-y=sin²x．

解析： 由通解形式写出特征方程，得对应齐次微分方程．由特解求出非齐次项f(x)．