问题
问答题
设y(x)＞0，y(0)=1，y’(0)=1，又曲线y=y(x)是单调的，凹凸性不变，且其上任意点处的切线及y轴和y=y(x)所围成的平面图形的面积等于切点处横坐标的三次方．求L的方程．
答案
参考答案：此题是基于积分给出数量关系的微分方程的求解问题，应特别注意由曲边梯形面积确定数量关系的正确性．
任意点P的坐标为(x，y)，如图其切线方程为曲边三角形的面积．
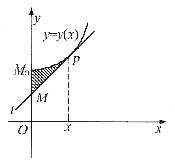
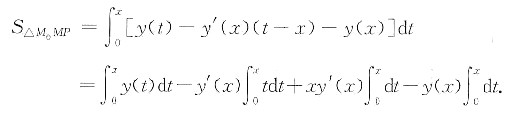
根据题设，有
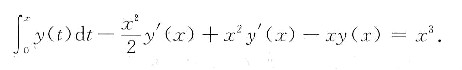
两边对x求导，得
y"=6，
y=3x2+c1x+c2．
由初始条件：y(0)=1，y’(0)=1，得c2=1，c1=1．
L的方程为
y=3x2+x+1．
当曲边三角形的面积
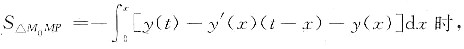则L的方程为
y=-3x2+x+1．
根据题设y(x)＞0，所以这个结果不符要求，舍去．
综合上述讨论，所求的L的方程为
y=3x2+x+1．
解析：[考点提示] 曲面积分问题．