问题
问答题
已知三元二次型
f(x1,x2,x3)=XTAX,
矩阵A的对角元素之和为3,且AB+B=0,其中
B=

若β=[4,-1,0]T,求Anβ
答案
参考答案:设β=k1α1+k2α2+k3α3,
解得k1=3,k2=-2,k3=1.
因此β=3α1-2α2+α,而Aα1=-α1,Aα2=-α2,Aα=5α,
故Anβ=An(3α1-2α2+α)=3Anα1-2Anα2+Anα
=3(-1)nα1-2(-1)nα2+5nα
=
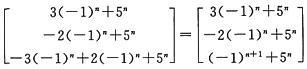
解析: 先由AB=-B,B=[α1,α2,α3]得到Aαi=-αi(i=1,2,3),从而求出A的部分特征值及其特征向量.再由主对角元素之和为3即可求出A的全部特征值,再由特征向量正交,求出其余的特征向量,再正交单位化,即可得到正交变换矩阵Q,从而可求出A,将β写成特征向量的线性组合即可求出Anβ,