问题
问答题
设总体X在区间[a,b]上均匀分布,求:(1)来自X的简单随机样本(X1,X2,…,Xn)的密度f(x1,x2,…,xn);(2)Y=maxX1,X2,…,Xn的密度fY(x);Z=minX1,X2,…,Xn的密度fZ(x).
答案
参考答案:(1) X的密度为F(x)=

由于X1,X2.…,Xn独立且与X同分布,所以有
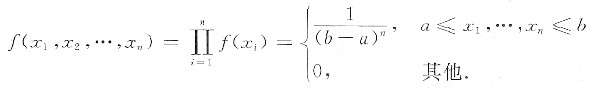
(2) 由题设x在[a,b]上服从均匀分布,其分布函数为
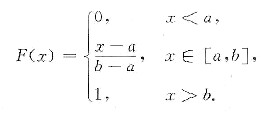
由Y=max{X1,X2,…,Xn)及Z=min{X1,X2,…,Xn)分布函数的定义,可知
FY(x)=[F(x)]n,
FZ(x)=1-[1-F(x)]n
于是有
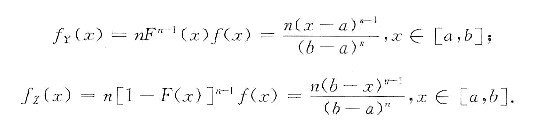
解析:[考点提示] 分布函数的密度问题.