问题
问答题
设f(x)在[a，b]上连续，且f(x)＞0，又
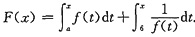
证明：
F(x)=0在[a，b]内有一且有一个实根．
答案
参考答案：因F’(x)≥2，故F(x)在[a，b]上单调增加，所以F(x)=0在[a，b]上至多有一个实根，又
F(a)=
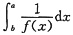＜0，F(b)=
＞0．由介值定理知，F(x)在[a，b]上至少有一个实根．
综上所述，F(x)在[a，b]上有一个且仅有一个实根．
解析：[解息] 利用F(a)＜0，F(b)＞0及介值定理证之．