问题
问答题
已知三元二次型
f(x1,x2,x3)=XTAX,
矩阵A的对角元素之和为3,且AB+B=0,其中
B=

用正交变换将二次型化为标准形,并写出所用的坐标变换
答案
参考答案:令β=[α1,α2,α3],αi为B的列向量,显然α1,α2线性无关,α3=α1+α2,因而r(B)=2,由AB=-B得到
A[α1,α2,α3]=-[α1,α2,α3],
即Aα1=-α1,Aα2=-α2,Aα3=-α3.
因α1,α2线性无关,故属于特征值-1的有两个线性无关的特征向量,所以λ1=λ2=-1为二重特征值.又因A的主对角线上的元素之和为λ1+λ2+λ3=3,故另一特征值为λ3=5.
设属于λ3=5的特征向量为α=[x1,x2,x3]T,则
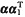 =0,
=0,
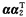 =0.
=0.
解
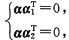 即
即

因
 ,
,
故α=[1,1,1]T.
对α1,α2进行施密特正交化得到
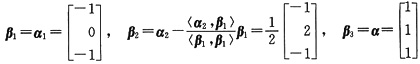 .
.
再将β1,β2,β3单位化,得到
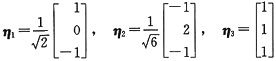 .
.
令Q=[η1,η2,η3],则Q为正交矩阵,且经正交变换X=QY后,二次型的标准形为
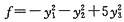 .
.

 缺失,
缺失, 单端固定桥修复,
单端固定桥修复, 牙周膜增宽,牙槽骨吸收至根长1/2,萌出正常,近中倾斜移位明显。
牙周膜增宽,牙槽骨吸收至根长1/2,萌出正常,近中倾斜移位明显。 单端固定桥
单端固定桥 半固定桥
半固定桥 单端固定桥
单端固定桥 活髓摘除后用桩冠恢复正常牙冠长轴后
活髓摘除后用桩冠恢复正常牙冠长轴后 固定修复
固定修复