问题
问答题
设

其中ai≠aj
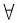 i,j=1,2,…,s.若B=ATA是正定矩阵,求s的取值.
i,j=1,2,…,s.若B=ATA是正定矩阵,求s的取值.
答案
参考答案:由于矩阵A的列向量为s个n维向量,如果s>n,则A的列向量组必线性相关,故存在X≠0,使AX=0,那么
XTBX=(AX)T(AX)=0,
与B正定相矛盾.
如果s=n,则因|A|是范德蒙行列式,
由
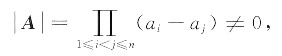
知A是可逆矩阵.由
B=ATA=ATEA,
即B与E相同,B是正定矩阵.
如果s<n,则取A的前s行构成的列向量组,从范德蒙行列式知其线性无关,那么延伸为n维向量后仍线性无关,故对任意的X≠0必有AX≠0,那么
XTBX=(Ax)T(Ax)=|AX|2>0,
B亦符合正定要求.可见B正定的充要条件是S≤N.
解析:[考点提示] 正定矩阵.
