问题
问答题
计算二重积分
(x2+y)dσ，其中D是由x2+y2=2y的上半圆，直线x=-1，x=1及x轴围成的区域．
答案
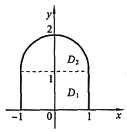
参考答案：解一 设
D1={(x，y)|-1≤x≤1，0≤y≤1}，
D2=((x，y)|x2+y2≤2y，y＞1}，
则D=D1∪D2，如下图所示．于是
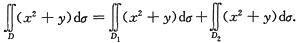
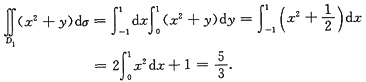
为计算
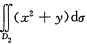，可引入极坐标
x=rcosθ，y-1=rsinθ，
于是D2={(r，θ)|0≤θ≤π，0≤r≤1}，
则有
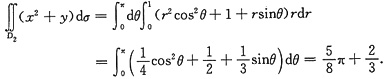
综上所述，
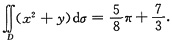
解二 直接把区域D写成不等式形式：
D={(x，y)|-1≤x≤1，0≤y≤
}，
从而
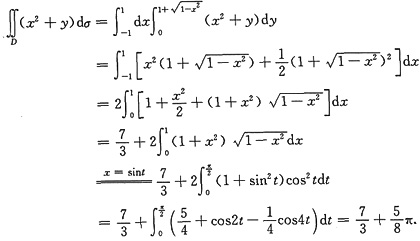
解析： 将积分区域D分为两部分，分别使用直角坐标和极坐标计算，或者直接在D上使用直角坐标计算．