问题
问答题
已知α1=(1,0,2,3),α2=(1,1,3,5),α3=(1,1,a+2,1),α4=(1,2,4,a+8),及β=(1,1,b+3,5).
(1) a,b为何值时,β不能表示成α1,α2,α3,α4的线性组合
(2) a,b为何值时,β有α1,α2,α3,α4的唯一的线性表示式并写出该表示式.
答案
参考答案:设x1α1+x2α2+x3α3+x4α4=β,按分量写出,则有
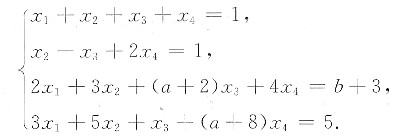
对增广矩阵高斯消元,有
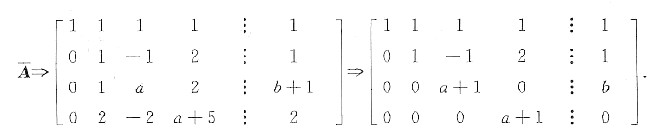
所以当a=-1,b≠0时,方程组无解,β不能表示成α1,α2,α3,α4的线性组合;
当a≠-1时,方程组有唯一解
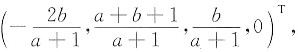 故β有唯一表示式,且
故β有唯一表示式,且
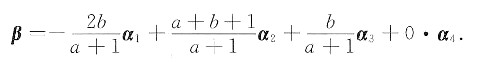
解析:[考点提示] 矩阵的线性表示.

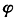
 为:()
为:()