问题
问答题
设f(x)在[a，b]上连续，且f(x)＞0，又
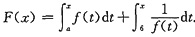
证明：
F’(x)≥2
答案
参考答案：[证明]
，
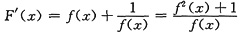由于[f(x)-1]2≥0，有f2(x)+1≥2f(x)，于是F’(x)≥2．
解析： 利用不等式a2+b2≥2ab证之；
搜题请搜索小程序“爱下问搜题”
设f(x)在[a，b]上连续，且f(x)＞0，又
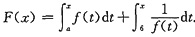
证明：
F’(x)≥2
参考答案：[证明]
，
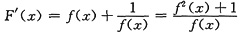由于[f(x)-1]2≥0，有f2(x)+1≥2f(x)，于是F’(x)≥2．
解析： 利用不等式a2+b2≥2ab证之；