问题
问答题
设A为n阶非奇异矩阵，α为n维列向量，b为常数，记分块矩阵
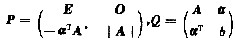
其中A*是矩阵A的伴随矩阵，E为n阶单位矩阵．
(Ⅰ)计算并化简PQ；
(Ⅱ)证明矩阵Q可逆的充分必要条件是αTA-1α≠b．
答案
参考答案：(Ⅰ)作分块矩阵乘法，并把A*A=|A|E，A*=|A|A-1代入，有
[*]
搜题请搜索小程序“爱下问搜题”
设A为n阶非奇异矩阵，α为n维列向量，b为常数，记分块矩阵
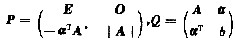
其中A*是矩阵A的伴随矩阵，E为n阶单位矩阵．
(Ⅰ)计算并化简PQ；
(Ⅱ)证明矩阵Q可逆的充分必要条件是αTA-1α≠b．
参考答案：(Ⅰ)作分块矩阵乘法，并把A*A=|A|E，A*=|A|A-1代入，有
[*]
