问题
问答题
设幂级数
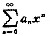在(-∞，+∞)内收敛，其和函数y(x)满足
y"-2xy’-4y=0，y(0)=0，y’(0)=1．
(Ⅰ)证明
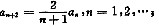
(Ⅱ)求y(x)的表达式．
答案
参考答案：(Ⅱ)为了求y(x)，要想通过解微分方程y"-2xy’-4y=0求得y(x)是不可取的，因为该方程是一个二阶变系数线性齐次方程，此类方程求解考研大纲不要求．我们可利用(Ⅰ)中得到的[*]及y(0)=O，y’(0)=1求得an表达式，然后进一步再求幂级数[*]的和函数y(x)．
[*]
将y，y’，y"代入y"-2xy’-4y=0得
[*]
则
[*]
解析：
[分析]： (Ⅰ)为了证明[*]只要将[*]利用等式两端同次幂系数相等便可得以证明．