问题
问答题
设f(u)具有二阶连续导数，而z=f(exsiny)满足方程
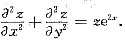
答案
参考答案：[解] 令u=exsiny，则
[*]
f"(u)=f(u)，即f"(u)-f(u)=0．
这是一个二阶线性常系数齐次微分方程，特征方程为r2-1=0，r=±1，则
f(u)=C1eu+C2e-u．
搜题请搜索小程序“爱下问搜题”
设f(u)具有二阶连续导数，而z=f(exsiny)满足方程
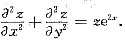
参考答案：[解] 令u=exsiny，则
[*]
f"(u)=f(u)，即f"(u)-f(u)=0．
这是一个二阶线性常系数齐次微分方程，特征方程为r2-1=0，r=±1，则
f(u)=C1eu+C2e-u．