问题
问答题
设二次函数f（x）=ax2+bx+c（a，b，c∈R，a≠0）满足条件：
（1）当x∈R时，f（x-4）=f（2-x），且f（x）≥x；
（2）当x∈（0，2）时，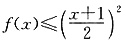
；
（3）f（x）在R上的最小值为0．
求最大的m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤x．
答案
参考答案：
∵f(x-4)=f(2-x)，∴函数的图象关于x=-1对称，
∴b＝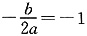
，
由(3)x=-1时，y=0，即a-b+c=0，由(1)得f(1)≥1，由(2)得f(1)≤1，∴f(1)=1，即a+b+c=1，又a-b+c=0，
∴
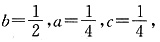
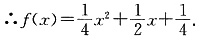
假设存在t∈R，只要x∈[1，m]，就有f(x+t)≤x．取x=1有f(t+1)≤1．即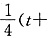
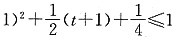，解得-4≤t≤0．对固定的t∈[-4，0]，取x=m，有f(t+m)≤m，即
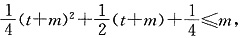化简有m2-2(1-t)m+(t2+2t+1)≤0，解得1-t-
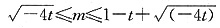于是有
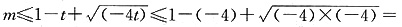9．当t=-4时，对任意的x∈[1，9]，恒有
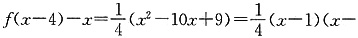9)≤0．所以m的最大值为9．