问题
问答题
设f(x)在0,1上可导且满足
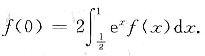
证明:至少存在一点ξ∈(0,1)使f’(ξ)+f(ξ)=0.
答案
参考答案:有两种讨论方式.
方法1.从结论推上去,要证明存在ξ∈(0,1)使
f’(ξ)+f(ξ)=0,
即eξf’(ξ)+eξf(ξ)=0,即证明存在ξ∈(0,1)使
(eξf(ξ))’=0.
命F(x)= eξf(x),要证存在ξ∈(0,1)使F’(ξ)=(eξf(x))’x-ξ=0.为此,只要验证F(x)在0,1上满足罗尔定理即可.由于
[*]
即 F(0)=F(η),0<η<1.
所以存在ξ∈(0,η)[*](0,1)使F’(ξ)=0,即
eξf’(ξ)+eξf(ξ)=0.
因eξ≠0,上式等价于f’(ξ)+f(ξ)=0证毕.
方法2.从条件往下推.由[*]及积分中值定理,存在[*]使f(0)=eηf(η),即e0f(0)=eηf(η).命F(x)=exf(x),有F(0)=F(η),由罗尔定理.存在ξ∈(0,η)[*](0,1)使[*]eξ(f’(ξ)+f(ξ))=0,即f’(ξ)+f(ξ)=0.证毕.
