问题
单项选择题
考虑一元函数f(x)的下列4条性质:
①f(x)在a,b上连续.
②f(x)在a,b上可积.
③f(x)在a,b上可导.
④f(x)在a,b上存在原函数.
以
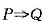 表示由性质P可推出性质Q,则有 ( ).
表示由性质P可推出性质Q,则有 ( ).

答案
参考答案:B
解析:
[分析]: 因可导必连续,连续函数必存在原函数,故(B)正确.
(A)是不正确的.虽然由①可推出②,但由②(可积)推不出③(可导).例如f(x)=|x|,在[-1,1]上可积:[*]但|x|在x=0处不可导.
(C)是不正确的.由②(可积)推不出④(存在原函数).例如
[*]
在-1,1上可积:
[*]
但f(x)在-1,1不存在原函数.因为如果存在原函数F(x),那么只能是F(x)=|x|+c的形式,而此函数在点x=0处不可导,在区问-1,1上它没有做原函数的“资格”.
(D)是不正确的.因为由③(存在原函数)推不出①(函数连续)。例子如下:
[*]
它存在原函数
[*]
但f(x)并不连续.即存在原函数的函数f(x)可以不连续.
