问题
问答题
设
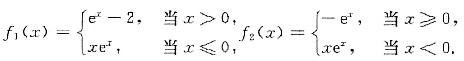 讨论f1(x)与f2(x)的极值.
讨论f1(x)与f2(x)的极值.
答案
参考答案:对于f1(x),当x>0时,f’1(x)=ex>0,所以在(0,+∞)内无极值.当x<0时,f’1(x)一(x+1)ex.命f’1(x)=0,得x1=-1.当x<-1时,f’1(x)<0,当-1<x<0时,f’1(x)>0.故f1(-1)=-e-1叫为极小值.再看间断点x=0处,x<0时f’1(x)>0;x>0且x充分小时,f1(x)<0,故f1(0)=0为极大值.对于f2(x),当x>0时,f’2(x)=-ex<0,所以在(0,+∞)内无极值.当x<0时,与f1(x)同,f2(-1)=-e-1为极小值.在间断点x=0处,f2(0)=-1.x>0时,f2(x)<-1;x<0且|x|充分小时,f2(x)为负值且|f2(x)<1,从而有f2(x)>-1.所以.f2(0)非极值.
解析:[注] 在可导的开区间内讨论极值用极值的必要条件以及极值的第一充分条件.在间断点处讨论极值,既不能用极值的必要条件(因为该处不可导),也不能用极值的第一充分条件(因为该处不连续),而应该用极值的定义,实际上用最原始的办法,将该点处的值与其附近的值比大小.读者可以画出f1(x)与,f2(x)的图看看就明白了.
