问题
问答题
将函数f(x)=arctan
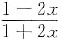 展开成x的幂级数,并求级数
展开成x的幂级数,并求级数
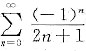 的和.
的和.
答案
参考答案:(1) 因为f’(x)简单,先求f’(x)的展开式,然后逐项积分得f(x)的展开式.
因
[*]
又f(0)=[*]两边积分得
[*]
因为f(x)在[*]处连续,
[*]
所以
[*]
(2) 令
[*]
又[*]因此[*]
解析:[考点提示] 求幂级数的和函数.
将函数f(x)=arctan
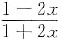 展开成x的幂级数,并求级数
展开成x的幂级数,并求级数
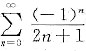 的和.
的和.
参考答案:(1) 因为f’(x)简单,先求f’(x)的展开式,然后逐项积分得f(x)的展开式.
因
[*]
又f(0)=[*]两边积分得
[*]
因为f(x)在[*]处连续,
[*]
所以
[*]
(2) 令
[*]
又[*]因此[*]
解析:[考点提示] 求幂级数的和函数.