问题
问答题
周长为2l的等腰三角形，绕其底边旋转形成旋转体，求所得体积为最大的那个等腰三角形．
答案
参考答案：
解析： 以等腰三角形的底边为x轴，以底边的中点作垂线为y轴，设等腰三角形的腰为a，底为b，则2a+b=2l，于是旋转体的体积为
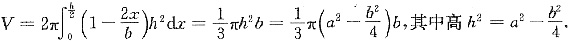
因为b=2(l-a)，所以
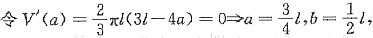因为是实际问题，极值点即为最大值点，故所得体积最大的那个等腰三角形的腰为
搜题请搜索小程序“爱下问搜题”
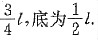
周长为2l的等腰三角形，绕其底边旋转形成旋转体，求所得体积为最大的那个等腰三角形．
参考答案：
解析： 以等腰三角形的底边为x轴，以底边的中点作垂线为y轴，设等腰三角形的腰为a，底为b，则2a+b=2l，于是旋转体的体积为
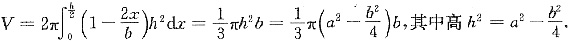
因为b=2(l-a)，所以
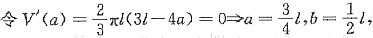因为是实际问题，极值点即为最大值点，故所得体积最大的那个等腰三角形的腰为
面深龋致牙髓炎，根管治疗后行铸造金属全冠修复，其临床牙冠短小，为最大程度地加强其固位力，最适方案是()