问题
问答题
设函数f(x)满足f(0)=1，
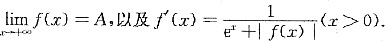
试证明：1≤A≤1+ln2．
答案
参考答案：[证] 由
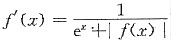可知f’(x)＞0，所以当x≥0时，有f(x)≥f(0)=1．
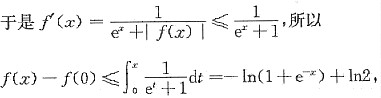
即f(x)≤1+ln2-ln(1+e-x)，即
1≤f(x)≤1+ln2-ln(1+e-x)．
在上式中令x→+∞，可得1≤A≤1+ln2．
搜题请搜索小程序“爱下问搜题”
设函数f(x)满足f(0)=1，
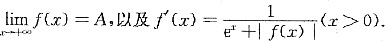
试证明：1≤A≤1+ln2．
参考答案：[证] 由
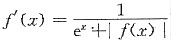可知f’(x)＞0，所以当x≥0时，有f(x)≥f(0)=1．
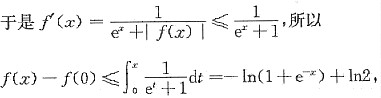
即f(x)≤1+ln2-ln(1+e-x)，即
1≤f(x)≤1+ln2-ln(1+e-x)．
在上式中令x→+∞，可得1≤A≤1+ln2．