问题
问答题
设f(x)，g(x)为有界闭区间[a，b]上的连续函数，且有数列
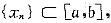使g(xn)=f(xn+1)，n=1，2，…．证明：
(Ⅰ)数列f(xn)，g(xn)都是单调递增的；
(Ⅱ)至少存在一点x0∈[a，b]，使得f(x0)=g(x0)．
答案
参考答案：[证] (Ⅰ)假设f(x1)≤g(x1)，则可推出，对任何自然数n，都有f(xn)≤g(xn)．否则就存在某个正整数n0。，使得f(xn0)＞g(xn0)，于是由f(x)，g(x)的连续性和介值定理可知，在x1和xn0之间至少存在一点x0∈[a，b]，使f(x0)-g(x0)=0，即f(x0)-g(x0)．从而命题成立．
考虑数列{f(xn))，因为对所有自然数n，都有
f(xn+1)=g(xn)≥f(xn)，
所以数列{f(xn))是单调增加的，同理数列{g(xn))也是单调增加的．
(Ⅱ)因为有界闭区间上的连续函数是有界的，所以数列{f(xn))，{g(xn))均有上界，从而它们的极限都存在，并且
即数列{f(xn)}，{g(xn))的极限都等于A
最后取数列{xn}的一个收敛子列{xnk}(在有界闭区间内这样的子列必然存在)，并设
=x0∈[a，b]，于是由f(x)，g(x)的连续性，有
