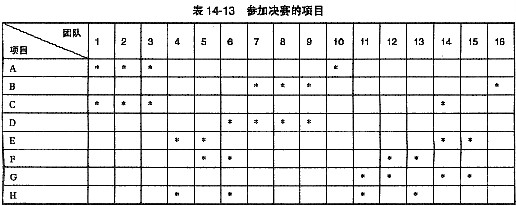
某学校运动会准备安排8个项目(命名为A,B,…,H)的决赛,16个团队(编号为1,2,…,16)参加决赛的项目如表14-13所示,“*”表示相应的团队将参加相应的决赛。
运动会组委会希望妥善安排这8个项目决赛顺序的方案,使每个团队不会连续参加两场决赛。针对表14-13的情况,这样的方案 (28) (提示:可在平面上将每个项目用一个点表示,在两个项目之间,只要有同一团队都参加,则在相应点之间用线连接)。
A.不存在
B.只有1个
C.共有2个
D.多于2个
参考答案:D
解析:
[分析]: 在平面上将每个项目用一个节点表示。每个团队参加的多个项目,在相应点之间都用线连接(已有连线时不用重复画)。即每两个项目,如有团队都参加,就在相应两点之间画连线(如图14-34(a)所示),表示这两个项目不能连续安排。为清晰起见,根据图14-34(a)再画一张连线状态相反的图(如图14-34(b)所示)。同样8个点表示8个项目,但图14-34(a)中两点之间有连线的地方,图14-34(b)中就没有连线;图14-34(a)中两点之间无连线的地方,图14-34(b)中就有连线。因此,图14-34(b)中的每条连线表示相应的两端项目是可以连续安排的。这样,只要在图14-34(b)中找到一条连线通路,正好将这8个点依次不重复地全都连接起来,就形成了一种可行的安排方案。
从图14-34(b)可以看出,依次连接这8个项目的通路有多条,例如:
E-D-A-F-B-G-C-H
G-B-F-C-E-D-A-H
F-C-D-F-A-E-B-G
上述每一条通路表示一种安排方案。按照其中任一方案,各团队都不会连续参加两场决赛。
[*]
