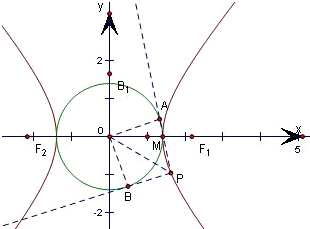
问题
选择题
过双曲线
|
答案
如图,∵
•PA
=0,∴PB
⊥PA
,PB
∴∠APB=90°,又PA=PB,PA,PB是圆的切线,
∴四边形OAPB是正方形,
∴OA=
OP=2 2
×22 2
=2,2
即
=2,∴m=4,m
又因为双曲线
-x2 m
=1(m>0,n>0)上的点P(y2 n
,-5
),3
∴
-5 m
=1,∴n=12,3 n
则该双曲线的离心率的值是
e=
=c a
=4+12 2
=2.16 2
故选C.