问题
问答题
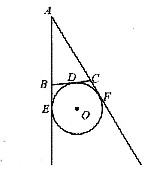
如图,在△ABC中,∠A所对的BC边的边长等于m,旁切圆⊙O的半径为R,且分别切BC及AB、AC的延长线于D,E,F.求证:
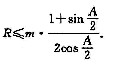
答案
参考答案:现对(1+sinA/2)/ (2cosA/2)化简令tanA/4=t则由万能公式:(1+sinA/2)/ (2cosA/2)=[1+2t/(1+t^2)]/[(1-t^2)/(2+t^2]=(1+t)^2/(2-2t^2)=(1+t)/(2-2t)=2*{(tanπ/4+t)/(1-tanπ/4*t)=2*tan(π/4+A/2)=1/2*cot(π/2-A/2)故原不等式即证明:a/R>=2*tan(π/2-A/2)连接:BO,CO,DO则有DO⊥BC DO=R令∠BOD=α ∠COD=βαβ均为锐角由于BO平分∠EODCO平分∠FODOE⊥EA OF⊥FA故有α+β=(π-A)/2同时a=BD+DC=Rtanα+Rtanβ=R(tanα+tanβ)故a/R=tanα+tanβ现证明:2tan【(α+β)/2】<=tanα+tanβ看这里吧:http://zhidao.baidu.com/question/61537776.html si=1故a/R=tanα+tanβ>=2tan【(α+β)/2】=2tan(π/2-A/2)
